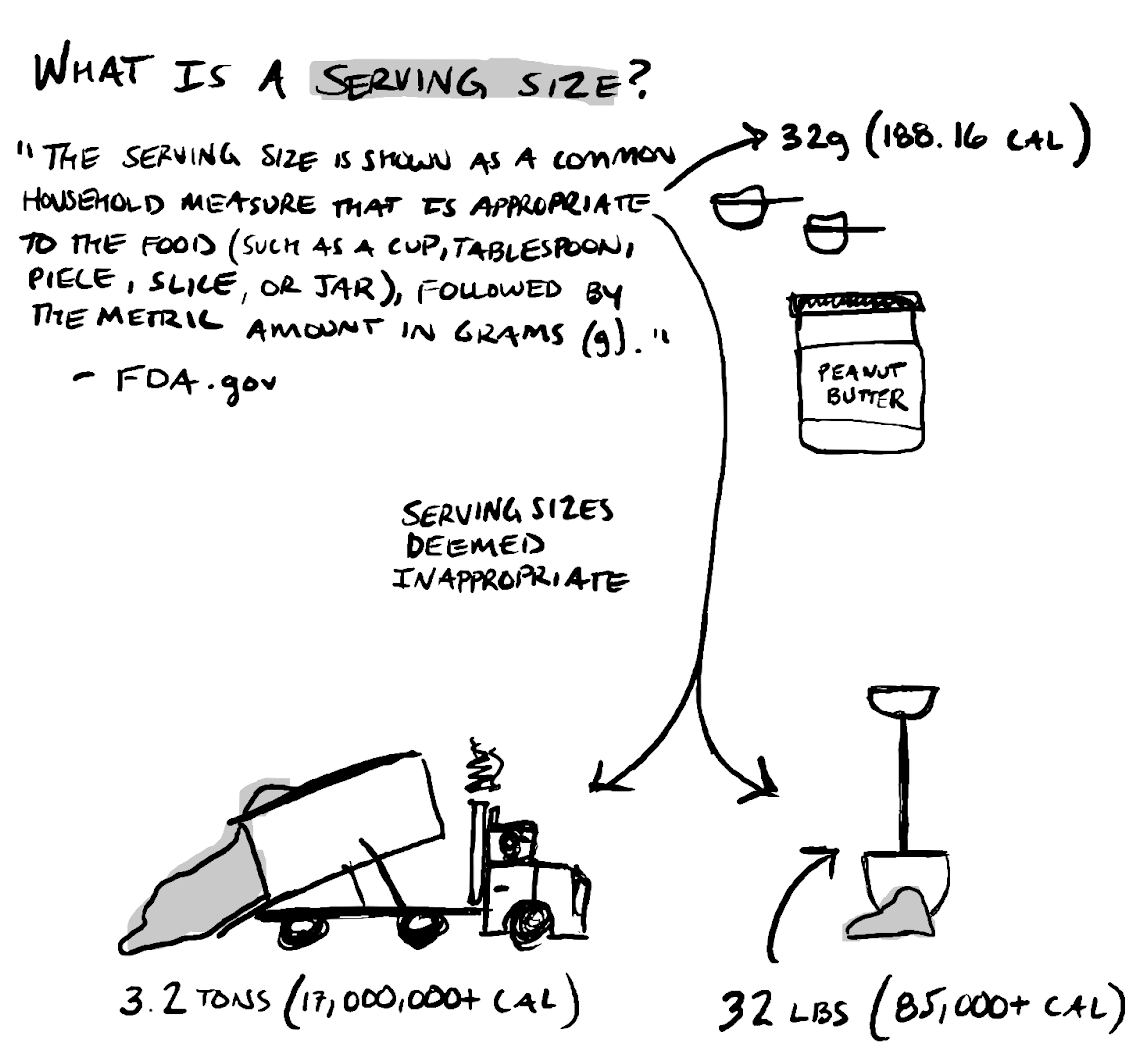
Use Nutrition Facts to calculate energy density.
Nutrition Facts are entirely useless, but they’re not useful in themselves. You need to make them useful in your analysis.
When confronted with food, there are many worthwhile questions to ask:
- Do I want this?
- What end goal am I aiming at by eating right now?
- Should I eat this particular food?
- Will I later regret eating this?
- Should I eat anything at all right now?
- What does it mean if I’m the sort of person who eats this?
- What will eat this do to me behaviorally?
- What will this food do for me? Will it provide energy, satisfy hunger, or meet nutritional needs?
- If I do eat this, how much of it should I eat?
- Will eating contribute to or hinder my flourishing?
- Am I bored?
Nutrition Facts can inform our response to these questions, but looking at the serving size won’t help much. There's some value in knowing that a serving of food might have 230 calories in it, but there’s much more value in knowing if those calories contribute to or take away from our well-being.
Energy density may be unfamiliar to you, but the concept isn’t. You already know that Red Delicious apples for $49/pound are a bad deal, but the same apples for $0.49/pound are a good deal. If this makes sense to you, then you already understand energy density.
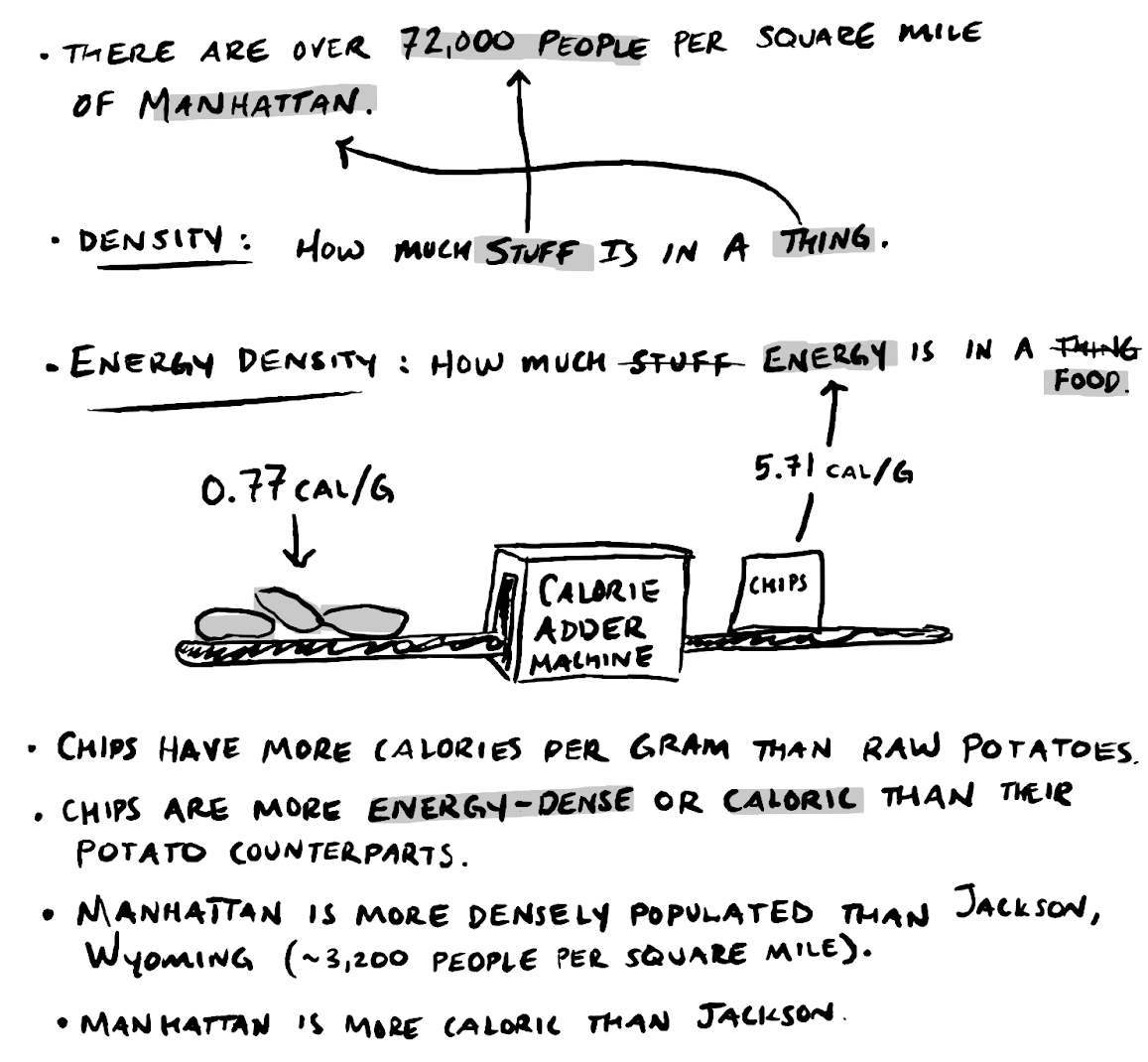
All we need to do is take the dollar-per-pound and map it to calorie-per-gram. If we ask a physicist to define energy density, the definition will be complex. But, for our project, energy density is as simple as cal/g.
The Nutrition Facts on a bag of potatoes tells me that a serving (a 180g potato) has 140 calories. The Nutrition Facts on a bag of chips says that a serving of 15 chips (28g) has 160 calories. Another way of using these facts is to calculate the energy density. For potatoes, it's 140 calories ÷ 180 grams = 0.77 cal/g. For chips, it’s 160 calories ÷ 28 grams = 5.71 cal/g.
One gram is a nebulous measurement. To make it concrete, I recommend picking one of the objects below. Then we can better appreciate that a cracker has 5.02 calories per gram and that grapes have 0.67 calories per gram.
 Previously I derived the energy density of potatoes and potato chips:
Previously I derived the energy density of potatoes and potato chips:
| Potato | 0.77 cal/g |
|---|---|
| Potato Chips | 5.71 cal/g |
If I eat a portion of potato chips as heavy as a birthday candle, it’ll cost 5.71 calories. The same birthday candle portion of potato costs only 0.77 calories. I have to eat over seven birthday candle portions of raw potato to get the same amount of calories as a single birthday candle portion of chips.
5.71 cal ÷ 0.77 cal/g = 7.41g

Potatoes are a better deal than chips. They give us more food for fewer calories. More than that, chips come with the catch that they are engineered to make you eat more. Although “getting a deal” isn’t the only consideration when purchasing something, it’s undoubtedly important.
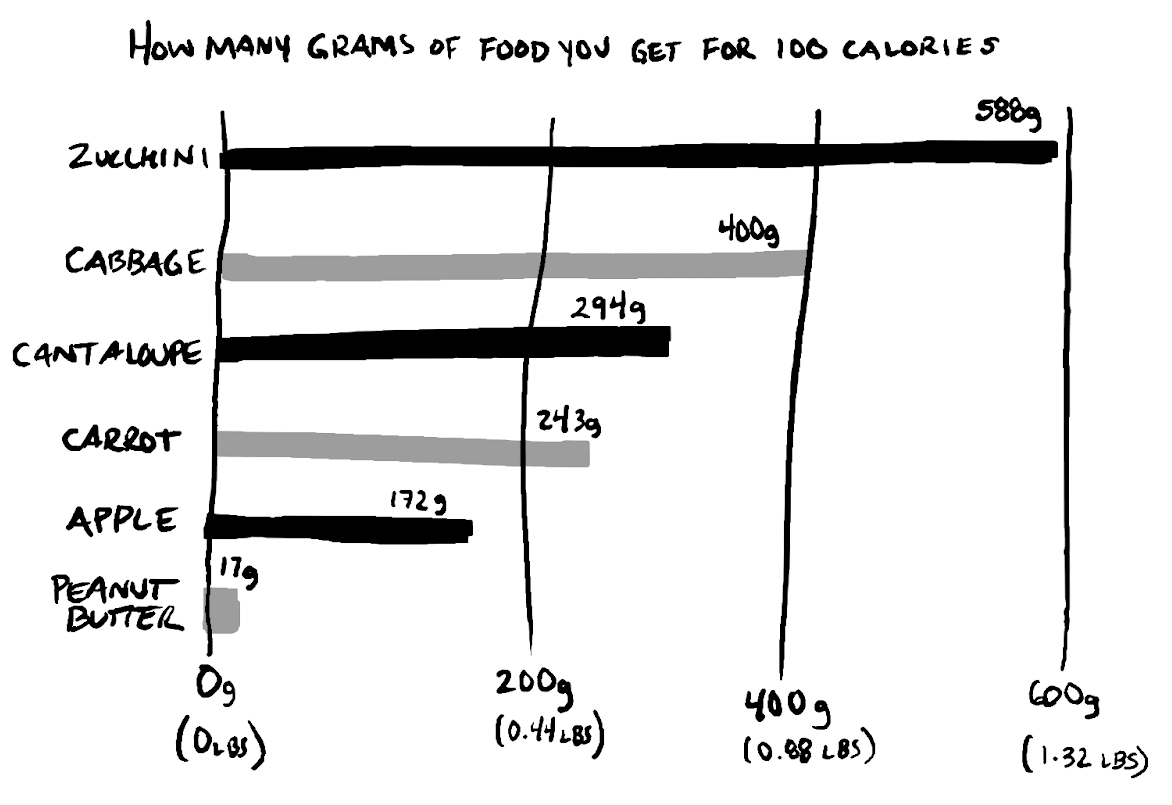
Let's say I have 100 calories to spend. What's a good deal for such a small amount? I can exchange them for 28 grams of cashews, amounting to about 11 cashews (0.06 lbs. or 1/16th of a pound). For the same "price" I could get 588 grams of zucchini (1.3 lbs). For every 1 gram of cashew I eat, I can eat 32 grams of zucchini.

Both options have equal amounts of calories but occupy unequal amounts of stomach capacity. We get more house when the price per square foot is lower.
Here’s a table of energy densities for four foods:
| Name | cal/g |
|---|---|
| Cabbage | 0.25 |
| Butternut squash | 0.45 |
| Cashews | 5.53 |
| Peanut butter | 5.88 |
We read energy densities like this: "5.88 calories per gram of peanut butter" in the same way you'd say "One dollar per pound of nectarines." Here’s energy density visualized another way:
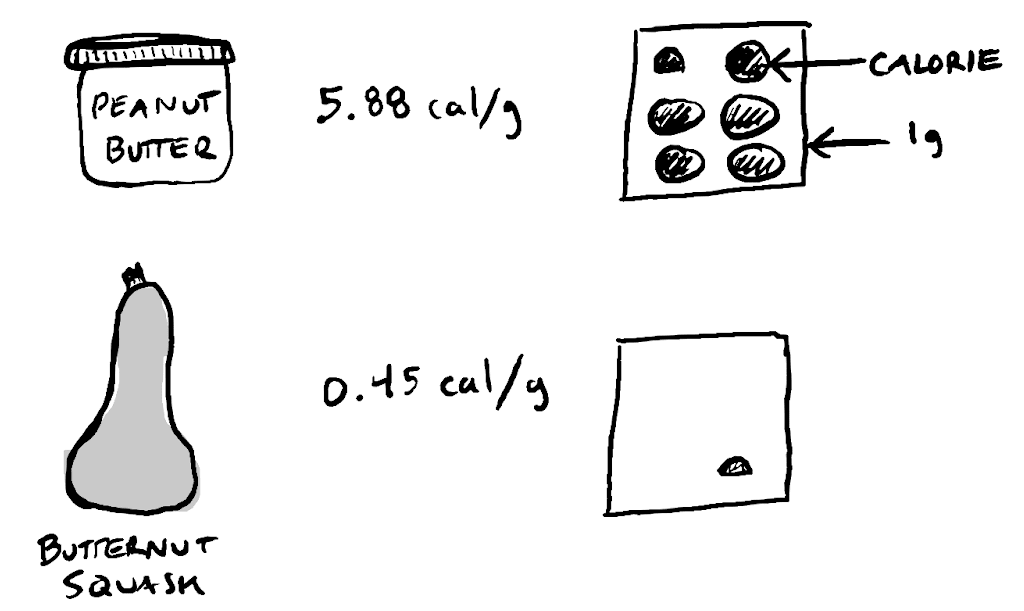
Energy density is a food’s price tag. Peanut butter is more expensive than butternut squash. For each 1 gram of peanut butter you eat, you could eat 13 grams of squash. If you spend 190 calories on peanut butter, you’ll get about 32 grams. You could eat nearly a pound of squash for the same price.
Eating well doesn’t mean eating as much as possible for as little as possible, but that we think before eating. Thinking, considering, and discerning are the human activities that make us fully alive.
Caloric foods need more consideration than low-calorie foods. They’re usually habit-forming and we’re more likely to blow our budget on them. Unconsidered pleasures tend towards excess. If we squander money, we gain debt. If we squander calories, we gain weight.
| Name | cal/g | cal/pound |
|---|---|---|
| Zucchini | 0.17 | 77 |
| Cabbage | 0.25 | 113 |
| Carrot | 0.41 | 185 |
| Apple | 0.58 | 262 |
| Mango | 0.6 | 271 |
| Potato | 0.77 | 348 |
| Banana | 0.89 | 403 |
| An oat-based cereal | 3.75 | 1,703 |
| Granola bar | 4.75 | 2,133 |
| Crackers | 5.02 | 2,278 |
| Potato chips | 5.35 | 2,428 |
| Peanut butter | 5.88 | 2,663 |